Chapter 1: Stern-Gerlach Experiments

Note

The hardest part of learning something new is not embracing new ideas, but letting go of old ones. ― Todd Rose, The End of Average: How We Succeed in a World That Values Sameness

Summary

Attention

The first steps we take in our exploration of the quantum mechanical world bring us at the doorstep of a key experiment, whose outcome cannot be explained by classical physics alone. The experiment was devised by Stern and Gerlach to study the intrinsic angular momentum of electrons. Stern-Gerlach (SG) experiments demonstrate that particles (i.e., electrons) do not behave classically.

First, the experiments indicate that the particles possess an angular momentum that is not classical (a classical momentum is called an orbital angular momentum arising from a particle that rotates, for example, as we will study in Chapter 10: Bound states of central potential). Judging from the experimental results, the spin angular momentum seems to present some properties of the classical angular momentum but also displays a drastically distinct behavior. For instance, its projection on a given axis takes discrete values (in our example, two of them only, as demonstrated in the first SG experiment).

Second, SG experiments highlight something even more peculiar: it seems impossible to know the projection of the non-classical momentum on different axes (e.g., $x$ and $z$ ) at the same time. This prompts us to develop a new formalism (a quantum mechanical formalism) to account for these behaviors. This leads us to introduce a quantum state vector (noted $\ket{\psi}$ and called ket) that includes all the properties of the system. Students will remember that the new notation (called the Dirac notation) should be a clear indication that we must adopt a new approach, in strong departure from classical physics. We also realize that the outcome of a measurement is probabilistic and we introduce the bra state vector (noted $\bra{\psi}$ ) that allows us to calculate probability amplitudes $\braket{\psi}{\phi}$ , which are complex numbers. The actual probability is the square modulus of the probability amplitude (that is: $|\braket{\psi}{\phi}|^2$ ). Finally, we know that the ket vectors live in the Hilbert space, with many properties similar to that of other spaces encountered more generally when learning linear algebra.

We also realize that if one considers all possible outcomes of the experiment (e.g., SGz where the projection on the $z$ axis is measured), we can build a complete set of basis vectors, which can be used to express any state vector (this is the principle of superposition). Because the interpretation is probabilistic, we are led to consider expectation values (noted $\expval{S_z}$ for the measurement of the momentum projected on the $z$ axis) and the uncertainty. It is important to realize that even though the mathematical description looks like that of a statistical analysis of large samples, the quantum mechanical interpretation applies to single particles.

What are the Stern-Gerlach (SG) experiments?

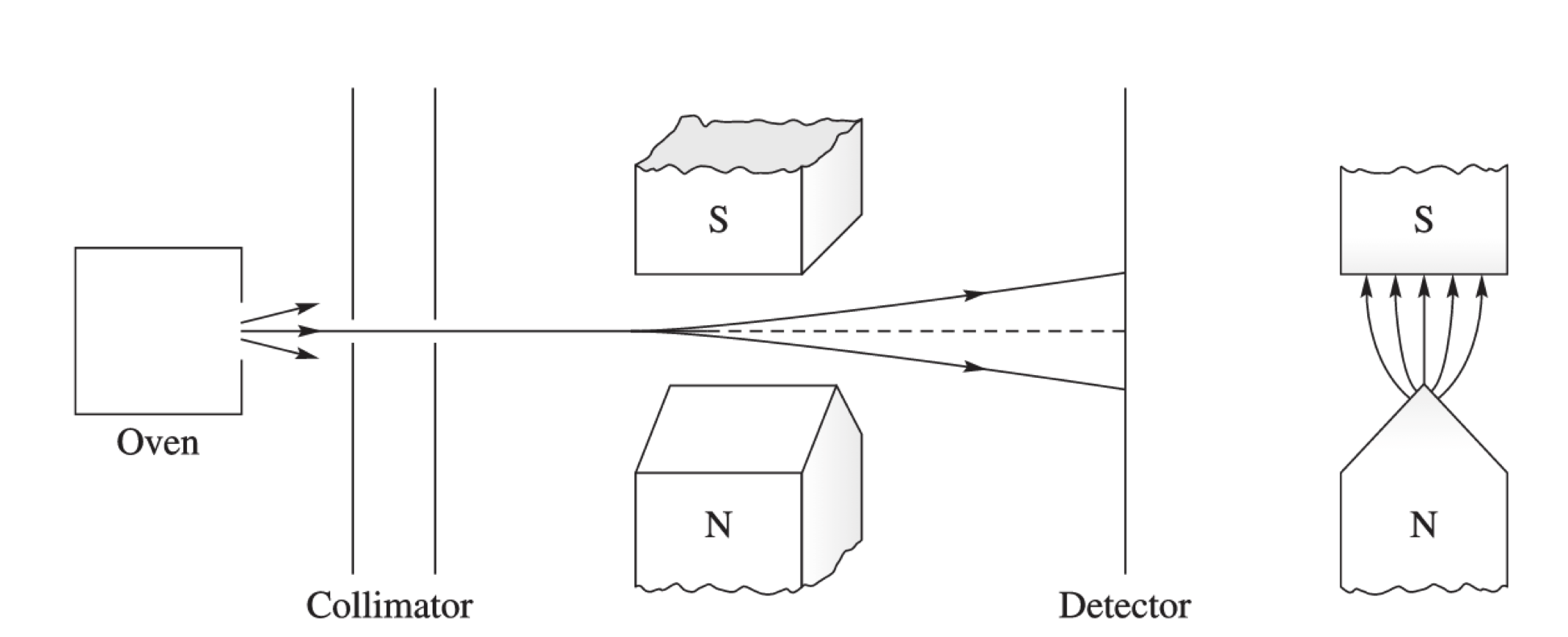
This apparatus allows for the measurement of the magnetic moment of a particle. The interaction between the magnetic moment and the external magnetic field provides a net force on the particle. It follows that the deflection of the particle can be used to determine the magnetic moment of the particle.

Important note: in order to generate a force, the magnetic field must be non-uniform as the force goes as:

$F_{z}=\mu \cdot \frac{\partial \mathbf{B}}{\partial z} \simeq \mu_{z} \frac{\partial B_{z}}{\partial z}$

It is essential to remember that in the SG experiments, the particle does not have a classical angular momentum so any deflection must be due to something else, which is not classical.

Through a series of SG experiments, one realizes that we must define a new framework, beyond classical physics, to try to account for those measurements.

Learning Material

Copy of Slides

The slides for Chapter 1 are available in pdf format here: 📂.

Screencast

Key Learning Points

Attention

The ket vector is noted as $\ket{\psi}$ , it is an abstract object. All the properties of the system it represents are included in it but it does not mean we have easy access to that knowledge.
The same information is included in the bra vector $\bra{\psi}$ . This vector lives in the reciprocal space and is introduced so that we can define the probability amplitude $\bra{\phi}\ket{\psi}$ (also called a projection or dot product), which is a complex number providing the probability amplitude of finding state $\ket{\psi}$ in state $\ket{\phi}$ .
The probability (a real number between 0 and 1) is given by the square modulus of the probability amplitude:

$P=|\bra{\phi}\ket{\psi}|^2$

This reads as “ $P$ is the probability of finding state $\ket{\psi}$ in state $\ket{\phi}$ ”. As a corollary, we have: that a proper state vector is normalized:

$|\bra{\phi}\ket{\phi}|^2=1$
The labels used to write the ket vectors indicate the knowledge we have acquired about the state, e.g., $\ket{+z}$ represents states that are deflected upward during the Stern-Gerlach experiment.
A complete basis is a set of ket vectors that can be used to express any other vectors. For instance, the only two possible outcomes of the Stern-Gerlach experiments are $\ket{+z}$ and $\ket{-z}$ . This means all vectors can be expressed using only those two vectors as the basis (this possibility is also referred to as the superposition principle). Mathematically, we translate this into:

$\ket{\psi}=c_+ \ket{+z} + c_- \ket{-z}$
Those coefficients are complex numbers and are given by projections on the basis vectors:

$|\psi\rangle=\underbrace{\langle+\mathbf{z} \mid \psi\rangle}_{c_{+}}|+\mathbf{z}\rangle+\underbrace{\langle-\mathbf{z} \mid \psi\rangle}_{c_{-}}|-\mathbf{z}\rangle$

7. An operator, in quantum mechanics is noted as $\hat{A}$ (that is: with a hat). It is a mathematical object that, when applied to a state vector, yields another state vector.

The expectation value of an operator $\hat{A}$ (that is: the average value you would measure when performing an experiment that corresponds to the operator is noted $\expval{\hat{A}}$ .
The uncertainty on the measurement of an operator $\hat{S}_z$ is

$\Delta S_{z}=\sqrt{\left\langle S_{z}^{2}\right\rangle-\left\langle S_{z}\right\rangle^{2}}$

For instance, in the Stern-Gerlach experiment on a spin-1/2 particle, the uncertainty is $~\hbar/2$ since the average value is zero and the only two possible outcomes are $\pm \hbar/2$ with identical probability.
An important outcome of the SG experiment is that it is not possible to know the value of the projection of the spin of particle along $x$ and $z$ at the same time. This can be seen by the fact that when using one outcome of the $SG_z$ apparatus as input of an $SG_x$ apparatus will always yield two possible outcomes with equal probability.

Test your knowledge

Why does an electron get deflected during a Stern-Gerlach experiment?
1. because of the electric field generated by the magnet.
2. because of the presence of a uniform magnetic field and the fact the electrons have a magnetic moment.
3. because of the presence of a non-uniform magnetic field and the fact the electrons have a magnetic moment.
4. None of the other answers is correct.
What do we learn from the Stern-Gerlach (SG) experiments?
1. Electrons behave classically for the most part.
2. Electrons have an intrinsic magnetic moment even when their (classical) orbital momentum is zero.
3. An electron seems to have a quantum mechanical angular momentum, distinct from its orbital angular momentum and that momentum can take any continuous value between a maximum and a minimum.
What is a ket vector $\ket{\psi}$ ?
1. It is a mathematical or abstract object that describes a given system. All of the information about the system is included in it, though one does not necessarily have easy access to that information.
2. It is a mathematical or abstract object that describes a given system. It includes some information about the system: the information one has already obtained with a measurement.
3. A ket vector is just a wave-function.
What is a bra vector $\bra{\psi}$ ?
1. It is a mathematical object that has very little use outside of IQM.
2. It is a mathematical object that approximately represents the corresponding ket vector $\ket{\psi}$ .
3. It is a mathematical object that includes the exact same information on the system as the corresponding ket does. However, it “lives” in a different space and it allows IQM students to perform dot products.
In the context of SG experiments, how do you translate this in English: $\braket{+z}{+x}$ ?
1. Smaller plus z vertical bar plus x larger.
2. Probability amplitude of finding a state $\ket{+x}$ in state $\ket{+z}$ after an SG $_x$ measurement.
3. Probability of finding a state $\ket{+x}$ in state $\ket{+z}$ after an SG $_x$ measurement.
A quantum state is defined up to an arbitrary phase factor. Said equivalently: mathematically the kets $\ket{\psi}$ and $e^{i\delta}\ket{\psi}$ (where $\delta$ is a real number) represent the same physical system.
1. True
2. False
When we say that $\{ \ket{+x},\ket{-x}\}$ represents a complete basis, what do we mean?
1. That the outcome of an SG $_x$ measurement can be any combination of $\ket{+x}$ , $\ket{-x}$ .
2. That any state $\ket{\psi}$ can be described as a superposition of $\ket{+x}$ and $\ket{-x}$ .
What are the expectation value and uncertainty of a measurement of SGz for this state: $\ket{\phi}=\frac{1}{\sqrt{3}}\ket{+z}+\sqrt{-\frac{2}{3}}\ket{-z}$ ?
What is the expectation value of a measurement of SGz for this state: $\ket{\phi}=\frac{1}{\sqrt{3}}\ket{+x}-\sqrt{\frac{2}{3}}\ket{-x}$ ?

(for this question, you can use the fact that $\ket{\pm x}=\frac{1}{\sqrt{2}}(\ket{+z}\pm\ket{-z})$ .
Calculate the expectation value and uncertainty for a measurement of SGZ for the following states: $\ket{\phi}=\frac{1}{\sqrt{4}}\ket{+x}-A\ket{-x}$ (hint: first determine the value of $A$ to ensure that the state is a proper state).
$\ket{\phi}=\frac{1}{\sqrt{3}}\ket{+y}-\sqrt{\frac{2}{3}}\ket{-y}$ .
$\ket{\phi}=\frac{1}{\sqrt{3}}\ket{+y}-A\ket{-x}$ (hint: there is no typo in this question!).

Hint

Find the answer keys on this page: Answers to selected test your knowledge questions. Don’t cheat! Try solving the problems on your own first!

Homework Assignment

Solve the following problems from the textbook: 1.3; 1.4; 1.5; 1.8, 1.11, 1.15