Lecture 12: The partition function

Note

The laws of thermodynamics, as empirically determined, express the approximate and probable behavior of systems of a great number of particles, or, more precisely, they express the laws of mechanics for such systems as they appear to beings who have not the fineness of perception to enable them to appreciate quantities of the order of magnitude of those which relate to single particles, and who cannot repeat their experiments often enough to obtain any but the most probable results. – J.W. Gibbs

Warning

This lecture corresponds to Chapter 20 of the textbook.

Summary

Attention

When we introduced the Boltzmann factor (which provides the probability of a system to assume a given energy state, in the canonical ensemble), we noted that in order for the probability distribution to be mathematically acceptable, it has to be properly normalized to equal one. The normalization factor is known as the Partition Function:

$Z=\sum_{\alpha} e ^{-\beta E_{\alpha}}$

where

$\beta=\frac{1}{k_B T}.$

If one knows the energy states of a system, it is pretty straightforward to calculate $Z$ (see box below for the example of a harmonic oscillator). In practice, the issue is to know all the energy states of a given system. The rest of the course will present a number of such examples.

In this chapter, we demonstrate that once we know the partition function, we can essentially know all the thermodynamics properties of a system in equilibrium! This comes from the straightforward applications of differential operators. The main results are summarized in this table:

$\arraycolsep=1.4pt\def\arraystretch{2.2} \begin{array}{lll} &{\rm Function~of~state} & {\rm Statistical-mechanical~expression}\\ \hline\hline U & & -\frac{ d \ln Z}{ d \beta}\\ F & & -k_B T \ln Z\\ \hline S & =-\left(\frac{\partial F}{\partial T}\right)_{V}=\frac{U-F}{T} & k_B \ln Z+k_{ B } T\left(\frac{\partial \ln Z}{\partial T}\right)_{V} \\ p & =-\left(\frac{\partial F}{\partial V}\right)_{T} & k_{ B } T\left(\frac{\partial \ln Z}{\partial V}\right)_{T} \\ H & =U+p V & k_B T\left[T\left(\frac{\partial \ln Z}{\partial T}\right)_{V}+V\left(\frac{\partial \ln Z}{\partial V}\right)_{T}\right] \\ G & =F+p V=H-T S~~~ & k_B T\left[-\ln Z+V\left(\frac{\partial \ln Z}{\partial V}\right)_{T}\right] \\ C_{V} & =\left(\frac{\partial U}{\partial T}\right)_{V} & k_B T\left[2\left(\frac{\partial \ln Z}{\partial T}\right)_{V}+T\left(\frac{\partial^{2} \ln Z}{\partial T^{2}}\right)_{V}\right]. \end{array}$

In this chapter, we also study the combination of partition functions. This is related to the idea that a system can be described using subsystems that are combined together.

Formally, if a system is described by the contribution of two energy terms:

$E_{i, j}=E_{i}^{(a)}+E_{j}^{(b)},$

then the partition function is simply:

$Z=\sum_{i} \sum_{j} e^{-\beta\left(E_{i}^{(a)}+E_{j}^{(b)}\right)}=\sum_{i} e ^{-\beta E_{i}^{(a)}} \sum_{j} e ^{-\beta E_{j}^{(b)}}=Z_{a} Z_{b}.$

Students, be warned! If the two energy terms correspond to two aspects that are not independent, then one can’t simply add energy contributions.

What is really striking is that in our large table of formulas above, $Z$ usually appears as $\ln Z$ . This means that combining different contributions to the partition functions has an additive effect on the various functions of states. We can apply this, for instance, to the combination of $N$ magnetic moments immersed in an external magnetic field. If we assume the moments do not interact with each other, we can write the total energy as a sum of individual terms without any cross terms between magnetic moments. It follows that:

$Z_{N}=Z_{1}^{N}$

where $Z_1$ is the partition function of a single magnetic moment in a magnetic field (this is a 2-state problem).

This allows us to compute thermodynamic properties and, in particular an expression for the magnetization as a function of temperature:

$M=\frac{m}{V}=\frac{N \mu_{ B }}{V} \tanh \left(\beta \mu_{ B } B\right).$

At low field, this expression corresponds to Curie’s law, which we have already encountered before!

Note

Partition function of one-dimension harmonic oscillator (1D-HO)

Quantum mechanically, we know that the energy spectrum of the 1D-HO is given by:

$E_n=\left(n+\frac{1}{2}\right) \hbar \omega$

where $n=0,1,\ldots$ .

Therefore, the partition function is:

$Z=\sum_{\alpha} e^{-\beta E_{\alpha}}=\sum_{n=0}^{\infty} e^{-\beta\left(n+\frac{1}{2}\right) \hbar \omega}=e^{-\beta \frac{1}{2} \hbar \omega} \sum_{n=0}^{\infty} e^{-n \beta \hbar \omega}=\frac{e^{-\frac{1}{2} \beta \hbar \omega}}{1-e^{-\beta \hbar \omega}}$

We can now obtain a number of thermodynamical properties:

Internal Energy:

$U=-\frac{ d \ln Z}{ d \beta}=\omega\left(\frac{1}{2}+\frac{1}{ e ^{\beta} \omega-1}\right)$
Heat Capacity:

$C_{V}=\left(\frac{\partial U}{\partial T}\right)_{V}=k_B (\beta \omega)^{2} \frac{ e ^{\beta} \omega}{\left(e^{\beta} \omega_{-1}\right)^{2}}$
Helmholtz function:

$\quad F=-k_B T \ln Z=\frac{\omega}{2}+k_B T \ln \left(1- e ^{-\beta} \omega \right)$
Entropy

$S=\frac{U-F}{T}=k_B \left(\frac{\beta \omega}{\rho^{\beta} \omega-1}-\ln \left(1- e ^{-\beta} \omega\right)\right)$

It is most instructive to examine the plots of those functions as a function of temperature:

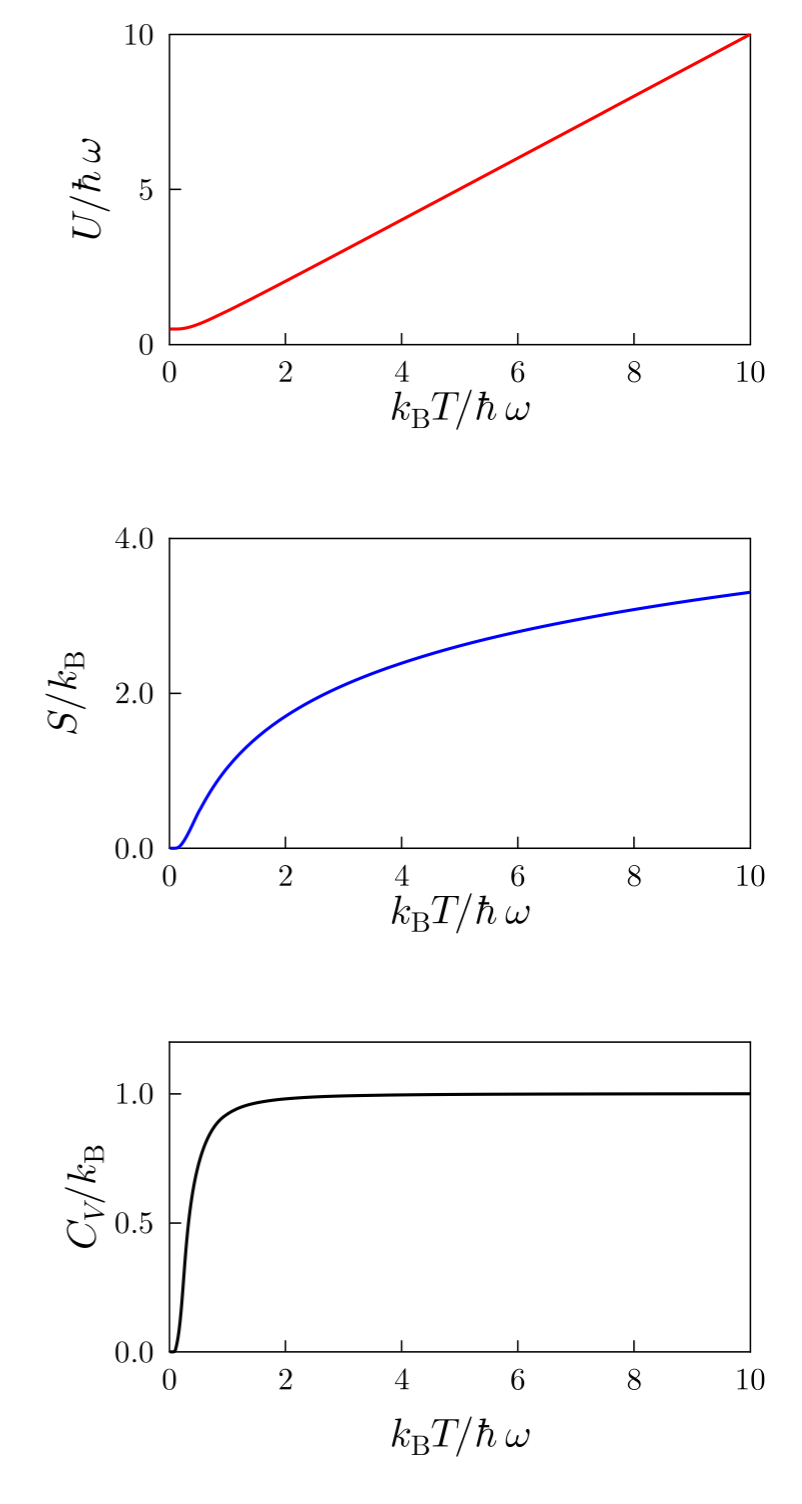
At low-temperature: (1) the internal energy coincides with the lowest energy of the harmonic oscillator since only the ground state can be occupied; (2) The entropy is zero since there is only one microstate; and (3) The heat capacity is zero as expected from what we learned in Lecture 10: Third Law of Thermodynamics.

At high-temperature: (1) the internal energy grows indefinitely since there is always an available state with higher energy; (2) the entropy keeps increasing as the number of microstates keeps growing; and (3) the heat capacity reaches a plateau: the limit is actually $C_v=k_B$ , as expected from the equipartition theorem. Indeed, since we have only two degrees of freedom (i.e., two quadratic forms for the potential and kinetic energy), the internal energy grows as $2\times k_BT/2$ and the first derivative with respect to $T$ yields the correct result (see Lecture 11: Equipartition of energy).

Key Definitions

Note

Two-level system:: A two-level system is a system in which individual particles can only take one of two possible energy values.

A full list of terms, including the ones provided here, can be found in the Index.

Learning Material

Copy of Slides

The slides for Lecture 12 are available in pdf format here: pdf

Screencast

Test your knowledge

What is the most accurate statement below regarding the partition function?
1. The partition function does not depend on the temperature and you need to know all the energy values a system can assume to calculate it accurately.
2. The partition function depends on the temperature and you need to know all the energy values a system can assume to calculate it accurately.
3. The partition function does not depend on the temperature and you do not need to know all the energy values a system can assume to calculate it accurately.
4. The partition function depends on the temperature and you do not need to know all the energy values a system can assume to calculate it accurately.
5. None of the other options is correct.
If you knew a partition function of a system exactly, you would be able to calculate all its thermodynamic properties.
1. True.
2. False.
3. It depends on the age of the captain.
Imagine you evaluate the partition function of a system of magnetic moments interacting with an external magnetic field. You treat this the same way they were treated when deriving Curie’s law: you suppose the magnets do not interact with each other. Do you expect the low temperature effects of an actual collection of magnets to be properly described?
1. Yes.
2. No.
3. It depends on how well you did on Exam 1.
Someone has calculated the exact partition functions ( $Z_a$ and $Z_b$ ) of single (isolated) atoms $a$ and $b$ . What is the partition function of a pair of atoms made up of one atom of type $a$ and one atom of type $b$ ? We suppose the two atoms do not interact.
1. $Z=Z_a+Z_b$ .
2. $Z=Z_a \times Z_b$ .
3. None of the other answers is correct.
Someone has calculated the exact partition functions ( $Z_a$ and $Z_b$ ) of single (isolated) atoms $a$ and $b$ . What is the partition function of a pair of atoms made up one atom of type $a$ and one atom of type $b$ ? The two atoms are placed in close proximity so that there is a net interaction between them.
1. $Z=Z_a+Z_b$ .
2. $Z=Z_a \times Z_b$ .
3. None of the other answers is correct.
If you have a system made up of $N$ non-interacting classical particles (each described by a partition function $Z_p$ ), what is the partition function of the system?
1. $Z=NZ_p$ .
2. $Z=(Z_p)^N$ .
3. $Z=Z_p/N$ .
4. $Z=Z_p^N/N!$ .

Hint

Find the answer keys on this page: Answers to selected test your knowledge questions. Don’t cheat! Try solving the problems on your own first!