Lecture 15: Photons
Note
Light is something like raindrops – each little lump of light is called a photon – and if the light is all one color, all the “raindrops” are the same. – Richard Feynman
Warning
This lecture corresponds to Chapter 23 of the textbook.
Summary
Attention
This lecture develops the following observation: any substance emits electromagnetic radiation at finite temperature. Our experience also tells us that the higher the temperature the more visible the light will be (here, we mean to say that the red-hot poker glows red while a body at room temperature emits in the infra-red).
We first use the first law of thermodynamics to find that the incident power per unit area is given, according to Stefan-Boltzmann law:
where
is a constant.
One aspect worth mentioning here is that we really treat the collection of photons as a gas and all the results we developed in this course so far for a gas are applied here. This is sometimes surprising to students as, when we talk about gas, they usually think about oxygen, nitrogen, etc. Here, the idea is that a gas is a collection of individual particles in a dilute form. This definition certainly applies to photons!
It is important to realize that the internal energy density of a
gas of photons in equilibrium with a cavity at temperature
is closely related to temperature:
where is another constant. Now, the big question is: what
kind of photons do we have to get this energy density? Using
Feynman’s word (see quote at top of this page): we know how much
“water” we have but we don’t know what type of raindrops we have in
it. For instance, a blue raindrop would be larger than a red
raindrop (in the allegory, blue is more energetic than red and thus
corresponds to a larger chunk of energy).
This central question is answered in the following by performing a statistical mechanics analysis. This leads to the black-body distribution, which can be expressed in terms of angular frequency:
or wavelength:
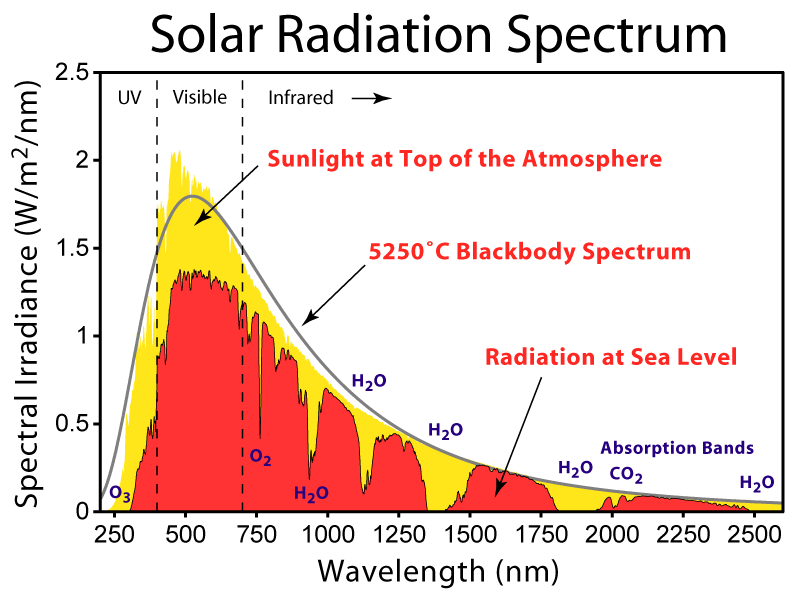
Figure obtained from i.sstatic.net/yTUFf.png
The black-body radiation can be applied very broadly to many systems. For instance, the Sun and the Earth are well described by the equations above. In the figure below we compare the radiation from the Sun (right above the Earth’s atmosphere, before molecules present in the atmosphere got a chance to absorb solar energy – red curve). The Sun appears to radiate as a body at 5800 K.
We conclude this chapter with two topics: Rayleigh-Jeans and Wien’s laws.
Rayleigh-Jeans: This law was developed before the advent of quantum mechanics and predicted the so-called ultra-violet catastrophe: the law predicts a diverging amount of internal energy at small wavelength. At high-wavelength, RJ law matches the black body radiation law. The issue is that RJ does not take into account that there are more and more states available as we increase frequency (remember that high-frequency corresponds to large momentum values and the “shell” of available states increase as the square of the momentum). However, at the same time as the number of states increases, the likelihood they will be filled goes down even faster (Boltzmann’s distribution). The “catastrophe” is thus averted in the correct treatment.
Wien’s law: WL describes the peak position observed in the black-body spectrum (See figure above). Essentially, WL establishes that:
This allows for the determination of the temperature of a body so long as we can record its emission spectrum!
See the boxes below for additioanl context on the cosmic radiation and on Einstein’s A and B coefficients.
Note
Kirchhoff’s law
KL relates how well an object emits and absorbs EM radiation:
A good emitter (at a given wavelength) is a good absorber (at the same wavelength).
This is truly a conservation law: at equilibrium, the internal energy is a constant and, as result, any energy that is emitted must be absorbed from the surroundings to preserve the status quo.
Warning
What is a black body cavity?
One key concept introduced in this course is concerned with understanding black body radiation. Simply put, a black body is a body that is a perfect absorber at any wavelength. As a result: it does appear black (no reflection or transmission). Following Kirchhoff’s rule: “a good absorber is a good emitter (at a given wavelength)”, a black body is also a perfect emitter. This is always very confusing to students: a black body is a perfect absorber in the sense that it neither (1) reflects nor (2) transmits any light. So, if you shine any light to a black-body, it will not reflect or transmit energy: it is perfectly black.
The confusion in student’s mind comes from this frequent
observation: “if the body emits perfectly, why do we call
it black?”. This is where the word “black body” is
clearly a misnomer. But students should understand this
(or at least this is the modest goal of the
instructor): At finite temperature , a material
will have internal energy, according to the equipartition
theorem, proportional to
. A black body would
emit that energy perfectly in the form of radiation.
So “black” is the way the object looks like if you were to use a flashlight to find the object in a dark room! But the object would emit as well according to Stefan’s law.
Cosmic background radiation
In 1978, Penzias and Wilson won the Nobel Prize for their observation (in 1963-1965 ) of a uniform microwave emission coming from all directions in the sky. The spectral shape of this emission exhibits the distribution for black-body radiation of temperature 2.7K with a peak in the emission spectrum at a wavelength of about 1 mm. The radiation is uniform and isotropic. This is one of the key evidence supportijg the hot Big Bang model of the universe’s origin. It implies that there was a time when all of the Universe we see now was in thermal equilibrium.
Einstein’s A and B coefficients
If atoms are subjected to thermal radiation, the atoms can make transitions between different energy levels. The atoms are thus in contact with a radiation field. Three processes can take place: (1) Spontaneous emission (occurs even in the absence of an external field); (2) Absorption; and (3) Stimulated emission. The various processes are summarized in the figure, where the so-called “Einstein’s A and B coefficients” are highlighted as well. In the figure, the levels 1 and 2 are atomic states.
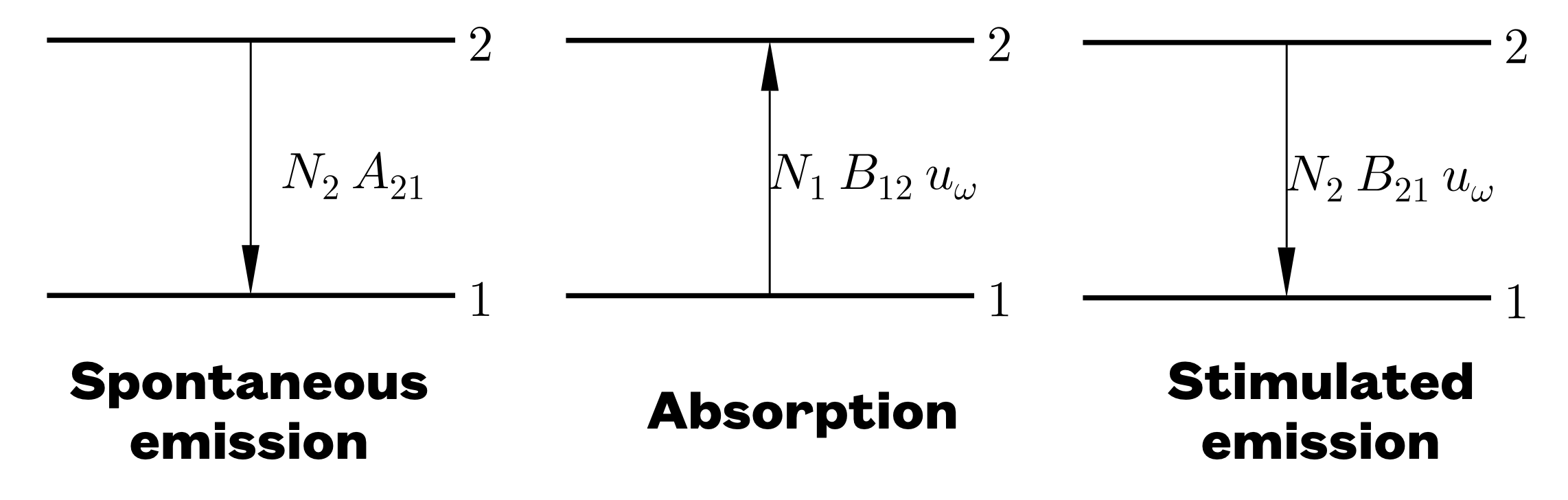
In order to get more photons produced than absorbed, a population inversion is needed so that the number of atoms (“the population”) in the upper state (per degeneracy level) exceeds that in the lower state. This is the principle of the laser (light amplification by stimulated emission of radiation). For laser operation, it is necessary to have further energy levels to provide additional transitions: these can provide a mechanism to ensure that level 2 is pumped and that level 1 can drain away.
Key Definitions
Note
- Cavity:
container of photons, which are themselves in thermal equilibrium with the cavity walls. From a wave-like perspective, the electromagnetic radiation forms standing waves in the confined volume.
- Diathermal material:
material that transmits heat between the gas of photons contained in a cavity and its surroundings.
- Spectral absorptivity (
):
is the fraction (dimensionless) of the incident radiation that is absorbed at wavelength
- Spectral emissive power (
)
of a surface is a function such that
is the power emitted per unit area by the electromagnetic radiation having wavelengths between
and
.
- Black body radiation:
radiation of a body with perfect spectral absorptivity at any wavelength. Due to Kirchhoff’s law, it is also a perfect emitter at all wavelengths.
- Black body cavity:
a cavity made up with black-body walls. It contains photons at same
as the walls, due to emission and absorption of photons by the atoms of the walls
- Dispersion relation:
this is a formal relationship
between a particle’s momentum and its energy. For instance, for a photon (or a phonon), the energy can be expressed in terms of frequency (
), so we also have
.
- Luminosity:
power per surface area times surface area
A full list of terms, including the ones provided here, can be found in the Index.
Learning Material
Copy of Slides
The slides for Lecture 15 are available in pdf format here: pdf
Screencast
Test your knowledge
- Any substance emits radiation so long as T>0.
True and the spectrum depends on the shape of the object.
True and the radiated energy distribution only depends on
.
True and the largest intensity of the radiation is in the infrared regime, regardless of the conditions.
False. Only substances that have been energized by an external excitation radiate.
- The temperature of a given substance is doubled. Therefore, the energy flux radiating from that substance, compared to the energy radiated at the initial temperature is multiplied by a factor of…
1/2
1/4
1/8
1/16
2
4
8
16
- A good emitter at a given frequency is a good absorber at any frequency. This statement is…
Always true
Generally false
- Thinking about the black-body radiation as described by Wien’s law, if the temperature of the black-body is doubled, what is the change in wavelength of maximal emission? (note: GRE-S question)
It remains the same
It is cut in half
It doubles
It quadruples
It is multiplied by 16
- When studying the radiative properties of the black-body using Rayleigh-Jeans theory, the ultra-violet catastrophe is due to
The fact measurements at high energy were not readily available in the early days of the twentieth century. The problem was resolved after physics students were asked to complete Exp. Phys. as a graduation requirement.
The fact high energy excitations are less likely than lower energy ones (as they require more energy). This is a quantum mechanical effect that was missing in the early model.
None of the other claims is correct.
Hint
Find the answer keys on this page: Answers to selected test your knowledge questions. Don’t cheat! Try solving the problems on your own first!
Homework Assignment
Solve the following problems from the textbook: