Lecture 3: Kinetic theory of gas, including Maxwell-Boltzmann

Note

With thermodynamics, one can calculate almost everything crudely; with kinetic theory, one can calculate fewer things, but more accurately; and with statistical mechanics, one can calculate almost nothing exactly. — Eugene Wigner

Warning

This lecture corresponds to Chapters 5, 6, and 8 of the textbook.

Summary

Attention

In this lecture, we first study the famous Maxwell-Boltzmann (M-B) distribution, which provides the probability distribution of the speed (i.e., length of the velocity vector) of a molecule in a gas, held at a given temperature. This is an important equation, and a number of results can be obtained from it as listed below. The equation reads:

$f(v) =\frac{4}{\sqrt{\pi}}\left(\frac{m}{2 k_{\mathrm{B}} T}\right)^{3 / 2} v^{2} \mathrm{e}^{-m v^{2} / 2 k_{\mathrm{B}} T}$

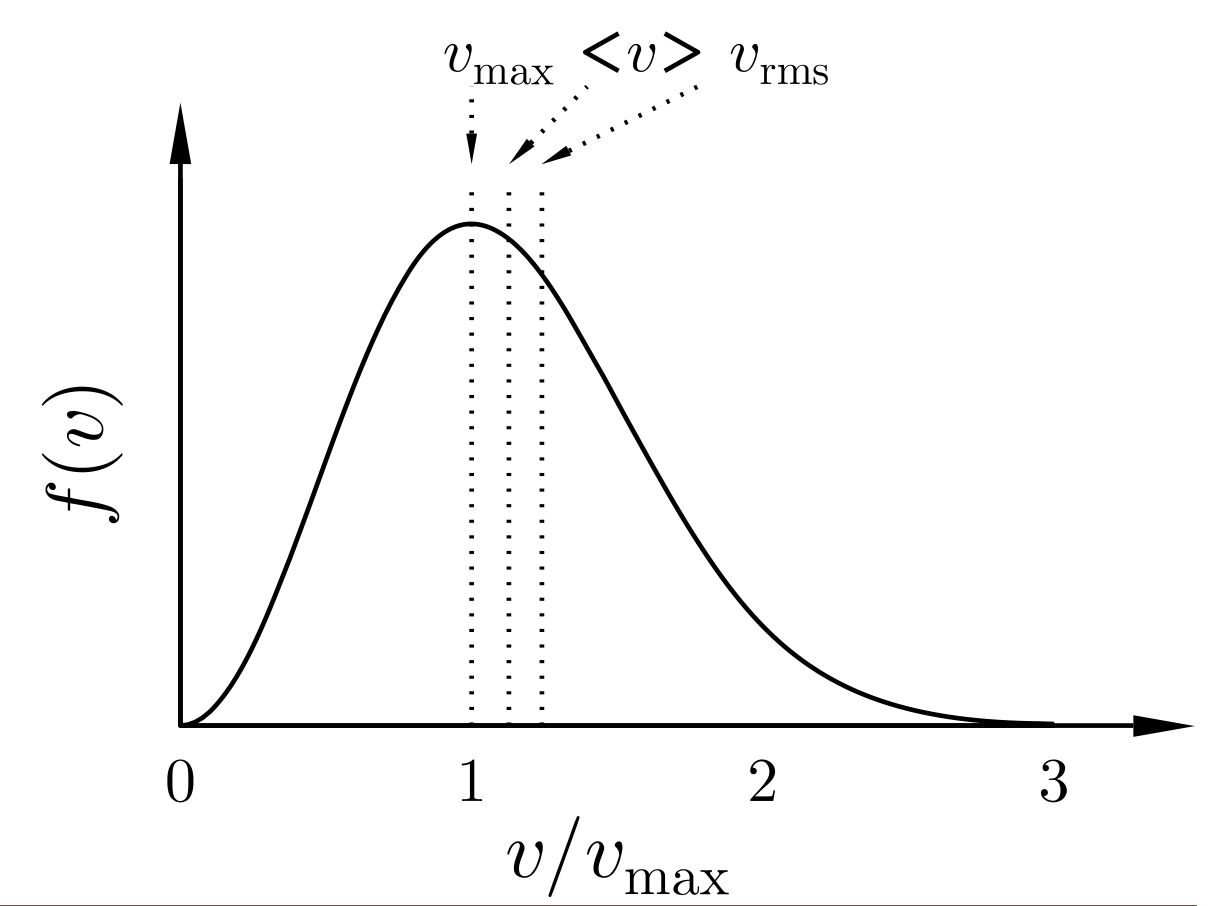
where we have the following expressions:

$\begin{aligned} v_{\max } &=\sqrt{\frac{2 k_{\mathrm{B}} T}{m}} \\ \langle v\rangle &=\sqrt{\frac{8 k_{\mathrm{B}} T}{\pi m}} \\ v_{\mathrm{rms}}=\sqrt{\left\langle v^{2}\right\rangle} &=\sqrt{\frac{3 k_{\mathrm{B}} T}{m}} \end{aligned}$

Using the M-B distribution, we compute the pressure of an ideal gas, calculated as the average force per unit area that a non-interacting gas exerts on a wall. This allows us to recover the ideal gas law! This is nice because, while the equation was first introduced as an empirical result, we know realize the condition of applicability: to have an non-interacting gas.

Learning Material

Copy of Slides

The slides for Lecture 3 are available in pdf format here: pdf

Screencast

Key Definitions

Note

Maxwell-Boltzmann distribution:

distribution of the speed of an ensemble of particles in contact with a heat reservoir kept at a temperature $T$ (canonical ensemble).

$f(v)=\frac{4}{\sqrt{\pi}}\left(\frac{m}{2 k_{\mathrm{B}} T}\right)^{3 / 2} v^{2} \mathrm{e}^{-m v^{2} / 2 k_{\mathrm{B}} T}$

rms speed:

The rms speed of a molecule at temperature T is given by

$v_{\mathrm{rms}}=\sqrt{\left\langle v^{2}\right\rangle}=\sqrt{\frac{3 k_{\mathrm{B}} T}{m}}$

Ideal gas equation:

$pV= Nk_{\rm B} T$

where $N$ is the number of molecules.

If one wishes to use the number of moles $n$ instead of the number of molecules, we have:

$pV= n R T$

where $R$ is the ideal gas constant.

Average kinetic energy:

$\left\langle v^{2}\right\rangle=\frac{3 k_{\mathrm{B}} T}{m}$

Corollary: since an ideal gas’ energy is only kinetic (because there is no interaction), the internal energy of an ideal gas only depends on temperature.

Pressure:

force per unit area (the force is normal to the surface).

Equation of state:

mathematical relationship between variable of states (example: the ideal gas law)

Kinetic theory of gas:

theory where the gas is modeled as being composed of a large number of particles (Bernoulli, 1700’s)

Solid angle:

angle, in three dimensions, subtended by of a portion of a sphere (a whole sphere has a solid angle of:math:4pi. It is expressed in steradians

Energy density:

this is the energy per volume of matter. The energy density of an ideal gas only depends on its pressure.

Mean free-path:

average time between two collisions between two particles in a gas.

Collision cross-section:

personal space of a molecule of gas: if another particle enters within the cross-section, it will interact with the molecule.

Collision time:

average time between two collisions for a given molecule in a gas.

A full list of terms, including the ones provided here, can be found in the Index.

Test your knowledge

The Maxwell-Boltzmann distribution…
1. is a method to rank Maxwell equations in Electromagnetic Theory by decreasing relevance as a function of a system’s temperature
2. provides information on the velocity vector distribution as a function of temperature
3. provides information on the speed (i.e., length of the velocity vector) distribution as a function of temperature
4. is a symmetrical distribution that can be expressed as a Gaussian distribution at any temperature
5. None of the other options is correct
According to Maxwell-Boltzmann distribution, we can determine that
1. the average kinetic energy of a gas molecule is $3/2k_BT$ regardless of the mass of the molecule
2. the average kinetic energy of a gas molecule is $3/2k_BT$ per unit mass of the molecule
3. the average interaction energy of a gas molecule is $3/2k_BT$ regardless of the mass of the molecule
4. the average interaction energy of a gas molecule is $3/2k_BT$ per unit mass of the molecule
5. None of the other options is correct
According to Maxwell-Boltzmann distribution, the expectation value of the speed of gas molecule at room temperature is
1. Rather slow, as found, e.g., in the Brownian motion
2. Moderately fast, a few cm/s
3. Quite fast, about the speed of sound in the atmosphere
4. Very fast, about the speed of light, making gas molecules almost relativistic
5. None of the other options is correct
According to the kinetic theory of gas and the ideal gas law, pressure is
1. linearly dependent on the mass of the molecules
2. proportional to its volume
3. inversely proportional to its temperature
4. proportional to its internal energy density
5. None of the other options is correct
We use the concept of ideal gas a lot in this course. Among these well-known gases, which one do you think behaves the most closely like an ideal gas?
1. Argon
2. (water) steam
3. Carbon monoxide
4. Nitrogen
5. None of the gas listed here behaves even close to an ideal gas
What is the hard sphere potential?
1. It is a potential that describes a gas as interacting billiard balls.
2. It is a potential that describes gas molecules as non-deformable billiard balls that only interact with other gas molecules when they touch
3. It is a potential that describes gas molecules as deformable billiard balls that only interact with other gas molecules when they touch
4. None of the other answers is correct.
What is the mean free path?
1. It is the distance a gas molecule moves during an infinitesimal time $dt$ .
2. It is the average time between collisions for a given molecule.
3. It is the average distance a molecule moves until it collides with another molecule.
4. The mean free path does not depend on the density of the gas

Hint

Find the answer keys on this page: Answers to selected test your knowledge questions. Don’t cheat! Try solving the problems on your own first!

Homework Assignment

Solve the following problems from the textbook: 2.5, 3.4, 4.2, 4.3, 4.4