Lecture 14: Chemical Potential

Note

Entropy is the price of structure – Ilya Prigogine

Warning

This lecture corresponds to Chapter 22 of the textbook.

Summary

Attention

In this chapter, we consider another natural variable: the number of particles in a given system. Just like we did at the beginning of our journey in this course, we will start with the internal energy and introduce a new concept that will enable us to consider the effect of changing the number of particles on the internal energy. Simply, we introduce the chemical potential which is the energy added to a system when a particle is added to that system:

${\rm d}U=T {\rm d}S-p {\rm d}V+\mu {\rm d} N.$

We see that the chemical potential is thus defined formally as:

$\mu_{i}=\left(\frac{\partial U}{\partial n_{i}}\right)_{S, V}.$

This can be used to find the useful relationship:

$\left(\frac{\partial S}{\partial U}\right)_{N, V}=\frac{1}{T} \quad\left(\frac{\partial S}{\partial V}\right)_{N, U}=\frac{p}{T} \quad\left(\frac{\partial S}{\partial N}\right)_{U, V}=-\frac{\mu}{T}.$

Just like we did before in Lecture 8: Thermodynamic potentials, we can use various constraints and the formal description shows that:

$\mu=\left(\frac{\partial F}{\partial N}\right)_{V, T}.$

In turn, based on results we obtained in Lecture 13: Statistical mechanics of an ideal gas, we see that for an ideal gas:

$\mu=k_{ B } T \ln \left(n \lambda_{ th }^{3}\right).$

Further manipulations on functions of state lead us to this other definition:

$\mu_{i}=\left(\frac{\partial G}{\partial n_{i}}\right)_{P, T}.$

The attentive student will realize that we are now dealing with slightly more complicated functions of state. This comes from the fact that we now need three natural variables to describe a given state. For instance, entropy, volume, and number of particles are the natural variables used to describe the total internal energy. One can also introduce a new function of state, known as the The Grand Potential. It is built similarly to the way one built the Helmholtz function but this time by also making sure that the natural variable is the chemical potential (rather than the number of particles):

${\rm d} \Phi_{ G }=-S {\rm d} T-p {\rm d} V-N {\rm d} \mu.$

The most important concept students will remember from this chapter is that the way the particles are transferred between two subsystems is governed by the second law of thermodynamics: the system will evolve (that is: exchange particles) until the chemical potential is uniform. It is useful to make a formal comparison with the case of two systems that are initially at different temperatures: when put in contact, the two systems will exchange heat until the temperature is uniform.

We will also remember that the chemical potential can be thought of as the Gibbs function per particle.

This formalism now allows us to study chemical reactions. In particular, we find that for an ideal gas:

$\mu(p)=\mu^{\ominus}+R T \ln \frac{p}{p^{\ominus}},$

where we defined standard pressure and temperature conditions using the symbol” $\ominus$ ”

For a chemical reaction, the equilibrium constant is obtained in terms of the change in Gibbs function:

$\ln K=-\frac{\Delta_{ r } G^{\theta}}{R T}.$

And, using the Gibbs-Helmholtz relation, we have:

$\frac{ d \ln K}{ d T}=\frac{\Delta_{ r } H^{\ominus}}{R T^{2}}.$

This last equation formalizes Le Chatelier’s principle: a system at equilibrium, when subjected to a disturbance, responds in such a way as to minimize that disturbance. Indeed, for a endothermic process, an increase of temperature will lead to a increase in the amount of products (larger $K$ ).

Finally, we introduce the concept of entropic forces, of which a couple of examples are illustrated in the blue boxes below.

Entropic versus energetic spring

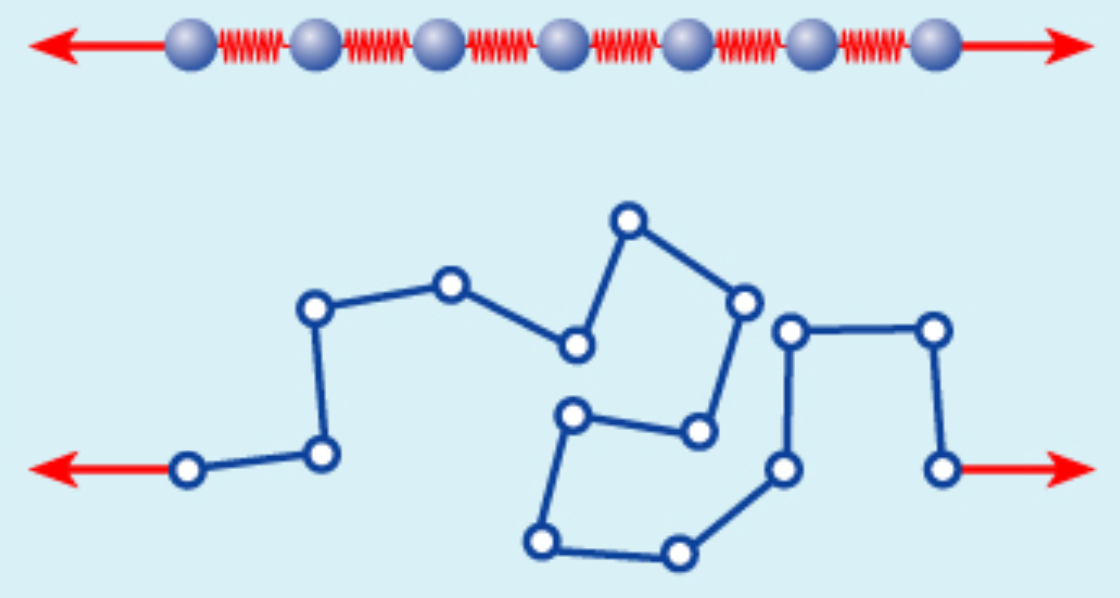
The example shown in the image is an illustration of the difference between a ‘classical’ and an ‘entropic’ force. In the first case, stretching the one-dimensional system is governed by Hooke’s law for each spring. In the second case, the difficulty to stretch the disordered spring comes from the fact that it is in a disordered configuration (with many microstates, thus a high entropy); while stretching it would decrease the entropy.

Osmosis

Osmosis is an illustration of the concept of entropic force. It is best understood using the figure below:

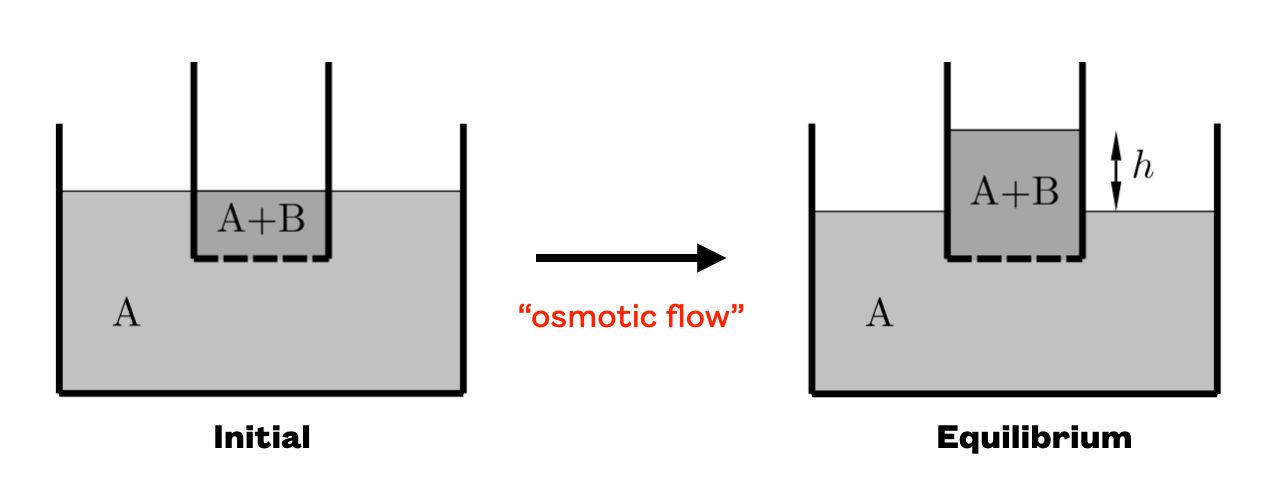
First, note that the small container has, at its bottom, a semi-permeable membrane (shown by dashed lines) that only allows the transport of ‘A’ components while ‘B’ are being blocked. The reason why the system evolves as it does, to the right, is due to the fact that the situation with the diluted “B” component corresponds to a much larger number of microstates than the initial situation. So, why does it stop at height $h$ ? Well, the column A+B will need to remain in equilibrium with the external pressure and the equilibrium will be reached when the pressure due to gravity is identical to the so called Osmotic pressure:

The number of applications of osmosis is large and of critical importance, especially in biology. Clearly there would be no life forms as we know them without the existence of entropy. Isn’t thermodynamics a wonderful subject?

Computational problem illustrating entropic force

This is a computational problem that will highlight the topic of “entropic force”. The problem is conceptually very simple. You have a bookshelf of length $L$ and you need to place $N$ statues of Einstein on it. You want to align them in a row on the shelf. The width of each identical statue is $2\sigma$ . For illustration purposes, use $N=15$ , $L=2$ , and $2\sigma = 0.1$ . But feel free to experiment with other values. The question is the following: what is the probability of finding a statue at position $x$ between $0$ and $L$ ? To answer this question, you will write a small computer code (it is indeed small!) where you will sample all “acceptable” possibilities.

A pseudo-code would be like this:

Pick $N=15$ positions randomly between $0$ and $L$
If any 2 positions overlap (within $2 \sigma$ ): reject the configuration (make sure the statue does not fall – watch out for the edges!)
If the sequence is acceptable, add the position to the “bins” of a histogram
Repeat this until you find a histogram that’s “converged” when normalized to the largest value (you will need to run this for at least $10^7$ loops in order to get maybe one or two acceptable picks! Report the rejection rate.

Does the result you find make sense? What happens if you add a cyclic boundary condition (that is: each end of the shelf is connected to the other one; hint: this is a small change in the algorithm)? The brute-force algorithm above is quite naive.

If you can come up with a better algorithm, you can earn an additional bonus point. (“better” is here defined as an algorithm will lower rejection rate).

Note added by VM: this is an adaptation of a problem described by Warner Krauth in his (wonderful) book Statistical Mechanics: Algorithms and Computations.

Key Definitions

Note

Chemical potential:

the chemical potential is the amount of energy added to a system when an additional particle of a given type is added to it; it is usually noted $\mu$ .

Equilibrium constant:

For a chemical reaction, one can write in all generality that the equilibrium constant is

$K=\prod_{j=1}^{p+q}\left(\frac{p_{j}}{p^{\ominus}}\right)^{\nu_{j}},$

where the $p_j$ ’s are the partial pressure of product/reactant $j$ . The $\nu_j$ ’s are the coefficients of the reaction: they are conventionally chosen as negative (reactants) and positive (products).

Micro canonical ensemble:

this is an ensemble of systems with the same energy.

Canonical ensemble:

ensemble of systems exchanging energy with a large heat reservoir; as a result these systems are held at constant temperature. This is the type of ensembles for which one can use the Boltzmann distribution.

Grand canonical ensemble:

ensemble of systems that can exchange both energy and particles with a large reservoir (this fixes temperature and chemical potential). For this type of systems, one uses Gibbs’ probability distribution.

Endothermic:

an endothermic reaction is a reaction that takes in heat. Using our convention, this means a positive heat exchange. This has to be contrasted with an Exothermic reaction, which releases heat (which takes on a negative sign).

Gibbs’ probability distribution:

This distribution applies to grand canonical ensembles:

$P(\epsilon, N) =\frac{e ^{\beta(\mu N-\epsilon)}}{\mathcal{Z}},$

where

$\mathcal{Z}=\sum_{i} e ^{\beta\left(\mu N_{i}-E_{i}\right)}$

is the Grand Partition Function.

van ‘t Hoff equation:

This equation provides a relationship for the change of equilibrium constant with temperature:

$\frac{ d \ln K}{ d (1 / T)}=-\frac{\Delta_{ r } H^{\ominus}}{R}.$

This equation clearly shows that the slop is proportional to the change in enthalpy under standard conditions.

Le Chatelier principle:

This principle establishes that a system at equilibrium, when subjected to a disturbance, responds in such a way as to minimize that disturbance.

A full list of terms, including the ones provided here, can be found in the Index.

Learning Material

Copy of Slides

The slides for Lecture 14 are available in pdf format here: pdf

Screencast

Test your knowledge

Among the definitions below, which one describes the concept of chemical potential the most closely?
1. The chemical potential represents the probability of a chemical reaction to take place.
2. The chemical potential quantifies the change in internal energy when one particle is added to a system.
3. The chemical potential is the heat transferred from (or to) a system when a chemical reaction takes place.
4. The chemical potential is the largest amount of work a system can do as the result of a complete chemical reaction.
When considering a process (such as a chemical reaction) when the number of particle $N$ changes, it is usual to use $N$ as a natural variable.
1. This is true even if we understand that calculating derivatives with respect to an integer value such as $N$ can give some headache to mathematicians.
2. This is true but we usually do not do this since the change in energy or entropy when the number of particles changes can be neglected.
3. This is not true since the first law of thermodynamics does not include cases where the number of particles can change.
4. I think I know what is going on but I’m not sure what the right answer is. I will therefore choose this option even though this would yield zero point for this question.
The second law of thermodynamics is clear: the entropy of a closed system always increases. Imagine two subsystems kept at the same temperature $T$ . The chemical potential on the left is $\mu_1$ and the chemical potential on the right is $\mu_2$ mu_1`. You now allow particles to move between the two subsystems. What is the most likely scenario? (to answer this question, remember that $\textrm{d}S=\frac{\mu_1-\mu_2}{T}\textrm{d}N$ where $\textrm{d}N$ is the number of particles moving from the left to the right.)
1. Particles will flow from the left to the right.
2. Particles will flow from the right to the left.
3. Nothing happens since the temperature is uniform.
What is a grand canonical ensemble?
1. That’s a great question. Thanks for asking it.
2. It is an ensemble with fixed temperature and chemical potential.
3. It is an ensemble with fixed temperature and number of particles.
4. It is an ensemble with fixed energy and temperature.
What is the relation between the Gibbs function and the chemical potential?
1. There is no connection between them.
2. The Gibbs function is the first derivative of the chemical potential with respect to temperature.
3. The chemical potential is the Gibbs function per particle.
The number of photons in vacuum is not a conserved quantity. Thus, the second law of thermodynamics translates into the fact that…
1. Their chemical potential is arbitrary
2. The number of photons will change until the chemical potential is zero at equilibrium.
3. The chemical potential is conserved.
What do we mean when we refer to standard values for pressure and temperature?
1. We refer to the instructor’s favorite soccer team in Belgium
2. We refer to pressure and temperature conditions typically found in a chemistry laboratory (i.e., $p=$ 1 Atm. and $T=$ 298K)
3. We refer to pressure and temperature values when a chemical reaction takes place
In the context of chemical reactions, what do we mean when we use the term molar?
1. We refer to quantities that are expressed in per mole units
2. We refer to quantities that are expressed in per molecule units
3. We refer to the fact students usually want to bite their thermodynamics homework all the way until the deadline for submission.
Consider the following equation: $\frac{\mathrm{d} \ln K}{\mathrm{d} T}=\frac{\Delta_{\mathrm{r}} H^{\ominus}}{R T^{2}}$ where $K$ is the equilibrium constant and the other variables are used in a way similar as we have done so far in this course. Based on that equation, what is the most accurate statement?
1. For an endothermic reaction, the reaction leans more to the right as $T$ increases
2. For an exothermic reaction, the reaction leans more to the right as $T$ increases
3. There is not enough information to draw definitive conclusions on this question.
Jacobus van ‘t Hoff…
1. wrote an equation that provides a link between the reaction rate and its enthalpy change
2. is a distant cousin of Stephen van Rensselaer and his equation states that more than 2 particles occupying a given container at (hopefully!) different times are more likely to cause a pandemic than 30 particles seated in a medium size container at the same time.
3. is a distant cousin of van der Waals but he worked on the hard-sphere potential rather than weak bonding.
4. None of the other answers is correct.
The concept of entropic force originates from
1. the gradient of the entropic potential.
2. the second law of thermodynamics and the maximization of entropy.
3. the need to give fancy names to elementary problems we learned in kindergarten.
4. None of the other answers is correct.
The existence of osmosis and the fact rubber cools when elongated are manifestations of…
1. The fact physics never ceases to amaze me.
2. Entropy can have macroscopic effects, including the emergence of forces that sometimes behave counter-intuitively.
3. The third law of thermodynamics, as the absolute zero of temperature cannot be met.
4. Two separate effects, both related to thermodynamics, but with nothing else in common.