Lecture 4: First Law of Thermodynamics

Note

Classical thermodynamics … is the only physical theory of universal content which I am convinced … will never be overthrown. — Albert Einstein

Warning

This lecture corresponds to Chapters 11 and 12 of the textbook.

Summary

Attention

In this lecture, we introduce the second law of thermodynamics and find that changes in internal energy can take place by a transfer of heat or work in or out of the system. Formally:

$dU = \dbar Q + \dbar W$

The notation above is loaded, and it is important to understand the “d-bar” we used there. A straight “d” refers to an exact differential, that is: its integration only depends on the starting and end points (this is called a function of state, since it only depends on the state rather than how we got there). Conversely, the “d-bar” refers to an inexact differential, that is: its integral between two states depends on the path taken. It follows that $Q$ and $W$ are not functions of state (that’s why we never actually use $Q$ or $W$ , and we use their changes instead). This is a crucial point that governs classical thermodynamics. Students should really spend some time making sure they understand this crucial point! More information can be found in Complement 1: Exact Differential.

In this lecture, we also studied two thermodynamic processes in greater details: the adiabatic expansion and the isothermal expansion of an ideal gas (see below for a definition of those terms). We were able to come up with two extremely important results that describe how to process translates in the $p vs. V$ phase diagram during the process.

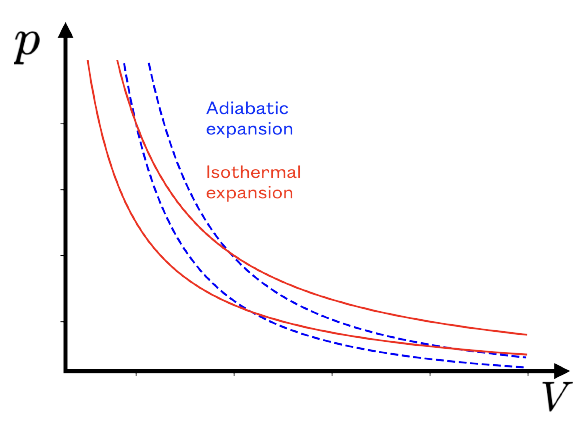
For an isothermic process: $pV=\textrm{constant}$ (the constant grows with temperature).

For an adiabatic process: $pV^{\gamma}=\textrm{constant}$ where $\gamma=c_p/c_V$ is a constant larger than one (it is 5/3 for an ideal gas).

Note also that during an adiabatic expansion, the temperature decreases (the reason is simple: during an expansion, work is done by the system, so it is negative; as a result, the total energy $U$ decreases and since, for an ideal gas, the internal energy is proportional to temperature, the temperature must decrease). More information on the sign convention can be found below.

During an isothermal expansion, for the same reason as the one given in the previous paragraph, the total energy is constant. This means that the work done by the system is negative (i.e., work done by the engine) and is exactly equal (in absolute value) to the heat transferred from the reservoir (the heat transfer is positive since it is transferred to the system, using our selfish sign convention).

Note

Sign convention

In this course, we will need to be careful about the sign of the heat transfers and work done. We will employ the usual selfish sign convention: $\Delta Q$ will be positive when heat is added to a system and $\Delta W$ will be positive when it is work done on a system.

It will happen that a different convention will be used (especially in Lecture 5: Second Law of Thermodynamics) where the positive sign will correspond to the arrows drawn on the figure. This should not cause any particular issue.

Learning Material

Copy of Slides

The slides for Lecture 4 are available in pdf format here: pdf

Screencast

Key Definitions

Note

Thermal equilibrium:: A system is in thermal equilibrium when its macroscopic observables (such as its pressure or its temperature) have ceased to change with time.
Function of state:: any physical quantity that has a well defined value for each equilibrium state of the system. Mathematically, a function of state corresponds to an exact differential.
Exact differential:: function whose integration between two given points does not depend on the path taken between the points. This definition is to be contrasted with the notion of inexact differential. Important examples of inexact differentials are: heat and work.
Internal energy:: is the sum of the energy of all the internal degrees of freedom that the system possesses. This is a function of state.
Thermally isolated system:: a physical system that cannot exchange heat with its surroundings.
Reversible work:: work performed on a gas at pressure $p$ is $\dbar W=-p \mathrm{~d} V$ .
Adiabatic index:: ( $\gamma$ ) is the ratio between the heat capacity at constant pressure and the heat capacity at constant volume. It is always larger than one, and 5/3 for an ideal gas.
Reversible process: A process that takes place: quasi-statically and for which the systems remain in equilibrium throughout the process. In reality, no actual process can be strictly reversible.
Isothermal expansion of a gas: an expansion taking place: in contact of a heat reservoir (i.e., at constant temperature).
Adiabatic expansion of a gas: an expansion taking place in: a thermally isolated container (i.e., without heat exchange with the surroundings).

A full list of terms, including the ones provided here, can be found in the Index.

Test your knowledge

What is a function of state?
1. A function of state is a function that describes the thermodynamic evolution of two systems in contact.
2. A function of state is a function that describes the state of a system, regardless how the system achieved it.
3. A function of state is a function that describes the state of a system, provided one knows how the system reached that state. distribution as a function of temperature.
4. None of the other options is correct.
The first law of thermodynamics states that:
1. Heat and work are two forms of energy that can be transformed from one into the other. The sum of the two types is constant.
2. Total energy is a conserved quantity, though work and heat contributions are not individually conserved.
3. Total energy is a function of state, work and heat are not.
4. All the provided definitions are correct.
A thermally isolated system…
1. Has constant temperature.
2. Has constant total energy.
3. Cannot exchange heat with its surrounding.
4. More than one option are correct.
5. None of the other options is correct.
The internal energy of an ideal gas…
1. Is uniquely defined if one knows its temperature.
2. Is uniquely defined if one knows its temperature and the volume it occupies.
3. Is dominated by internal interaction energy.
4. None of the other options is correct.
Compare the expansion of an ideal gas performed adiabatically and that performed isothermally. Consider the $p-V$ evolution.
1. $p(V)$ decays faster for the adiabatic process compared to the isothermal one.
2. $p(V)$ decays slower for the adiabatic process compared to the isothermal one.
3. The decay of $p(V)$ is always irreversible, even for a quasi-static expansion.
4. None of the other options is correct.

Hint

Find the answer keys on this page: Answers to selected test your knowledge questions. Don’t cheat! Try solving the problems on your own first!

Homework Assignment

Solve the following problems from the textbook: 2.5, 3.4, 4.2, 4.3, 4.4