Lecture 18: Real gas

Note

There can be no doubt that the name of van der Waals will soon be among the foremost in molecular science. – James Clerk Maxwell

Warning

This lecture corresponds to Chapter 26 of the textbook.

Summary

Attention

In this course, we have frequently used the equation of state of an ideal gas law. As a reminder, this law considered that each gas molecule is point-like (i.e., there are no collision between molecules) and do not interact (no attraction or repulsion). Of course, this may be realistic for a dilute gas where the average distance between molecules is large. But what happens when the density increases?

There are several models to provide a more realistic description of gases: van der Waals equation, Dieterici equation, and – more generally – the virial expansion.

The van der Waals equation reads as:

$\left(p+\frac{a}{V_{ m }^{2}}\right)\left(V_{ m }-b\right)=R T,$

where $V_m$ is the volume per mole, $a$ and $b$ model the attractive and repulsive parts of the equation.

It is always a good idea to make a plot when faced with a new concept described by an equation. Many times in this course, we plotted the isotherm of an ideal gas: it was the central concept involved in our understanding of the Carnot cycle.

For an ideal gas, the right-hand-side of the ideal gas equation:

$pV=nRT$

is a constant for an isotherm.

What changes in the realistic gas description?

Rearranging the equation shown in the summary, we have:

$p V^{3}-(p b+R T) V^{2}+a V-a b=0.$

This third-order polynomial can be plotted for various value of of $T$ and we find an important behavior that will be central to our understanding of phase transitions.

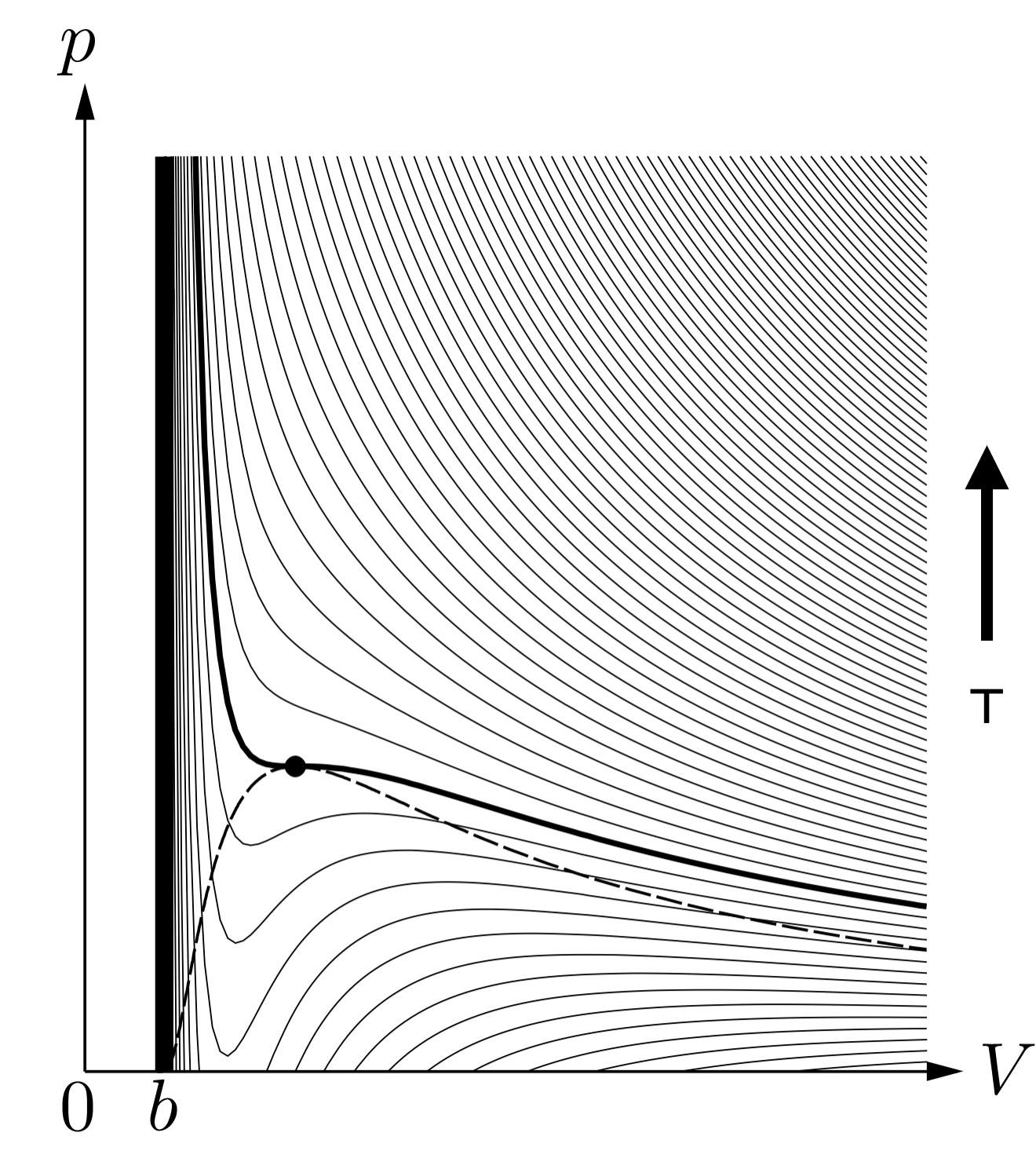
At high temperature, this equation reduces to the ideal gas law for large enough volume. However, a low-temperature, the description of the vdW equation is less and less like the ideal gas law. In fact, it starts to have an “S” shape, with a local minimum that gets deeper and deeper at the temperature is reduced.

The Critical temperature is the temperature at which a local minimum appears. Right at that point, there is an inflection point defined by:

$\begin{aligned} &\left(\frac{\partial p}{\partial V}\right)_{T}=-\frac{R T}{(V-b)^{2}}+\frac{2 a}{V^{3}}=0 \\ &\left(\frac{\partial^{2} p}{\partial V^{2}}\right)_{T}=\frac{2 R T}{(V-b)^{3}}-\frac{6 a}{V^{4}}=0. \end{aligned}$

At that point, the isothermal compressibility diverges:

$\kappa_{T}=-\frac{1}{V}(\partial V / \partial p)_{T} \rightarrow \infty.$

This effect does not occur using the ideal gas law since ideal gas law isotherms do not present any inflection point for any temperature.

Attention

One important figure to understand about existence of phases

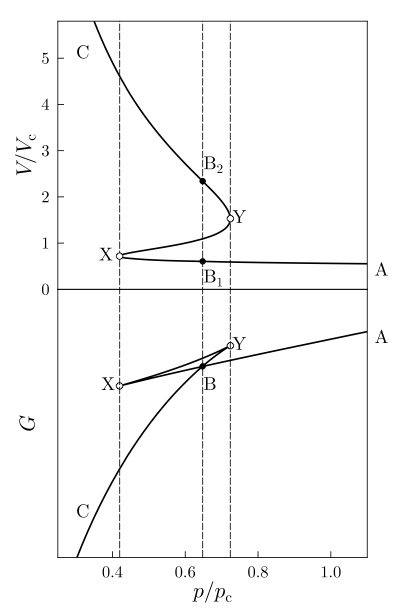
The figure on the left needs to be thoroughly understood. Let’s first focus on the top of the figure. This is an isotherm for a realistic gas, plotted for a value of the temperature below the critical temperature. This is why we see a clear minimum (Y) followed by a maximum (X). This figure is plotted as $V(p)$ while most of those figures were plotted as $p(V)$ so far in the course. This is done for convenience so we can simultaneously monitor how the Gibbs energy evolves as a function of pressure (bottom panel).

Gibbs is the appropriate function of state to consider here: we want to know what volume a system will take for a given temperature and pressure. Indeed, the $V(p)$ is a multi-valued function. So, we may wonder: what volume will be the one taken by the system at a pressure value around the B point? The answer: the one for which the Gibbs function will be the smallest.

What happens exactly at the point B? In that case the Gibbs function is equal for both B1 and B2 and two phases coexist: one with high compressibility (gas) and one with low compressibility (liquid).

Physically, it is possible that a system could be found on the segment BX (super-heated liquid) or segment BY (super-cooled gas). These states would correspond to transients for which the thermodynamic limit has not been reached yet.

Warning

Proper spelling

Here, we have been talking about “van der Waals” equation. The equation was studied by Diderik van der Waals, who was born on November 23, 1837 in Leyden, The Netherlands. In Dutch, van der Waals’ native language, the “van” is never capitalized unless it is used at the start of a sentence. A pet peeve of the instructor? Maybe due to the fact he learned Dutch for many years in high-school during his youth in Belgium!

Key Definitions

Note

Critical temperature:: Temperature under which isotherms of a real gas shows a minimum and a maximum. At the critical temperature, there is an inflection point corresponding to a diverging isothermal compressibility.
Dieterici equation:: Model of a realistic gas, described by the following equation (where the parameters have same definition as for the van der Waals equation):

$p\left(V_{ m }-b\right)=R T \exp \left(-\frac{a}{R T V_{ m }}\right).$
Virial expansion:: Model for a realistic gas using a Taylor expansion in $\sim \frac{1}{V_m}$ and where the zeroth order term corresponds to the ideal gas law.

$\frac{p V_{ m }}{R T}=1+\frac{B}{V_{ m }}+\frac{C}{V_{ m }^{2}}+\cdots$

A full list of terms, including the ones provided here, can be found in the Index.

Learning Material

Copy of Slides

The slides for Lecture 18 are available in pdf format here: pdf

Screencast

Test your knowledge

When would you say a gas can be described accurately by the ideal gas law?
1. At low density.
2. At high density.
3. At low pressure.
The van der Waals model for a gas:
1. includes both an attractive and a repulsive term.
2. only accounts for the finite size of the particles in the gas.
3. only accounts for the (large-distance) attractive potential between the particles.
4. only obeys social distancing but does not allow for attraction.
When using a realistic description of a gas, we find that:
1. two coexisting phases are possible under the critical point, they correspond to two phases that have the same pressure, same volume, and same Gibbs energy
2. two coexisting phases are possible under the critical point, they correspond to two phases that have the same pressure, different volumes, and same Gibbs energy
3. two coexisting phases are possible under the critical point, they correspond to two phases that have the same pressure, different volumes, and different Gibbs energy
4. two coexisting phases are possible under the critical point, they correspond to two phases that have different pressure, same volumes, and different Gibbs energy
Speaking about the virial expansion, in thermodynamics:
1. you can avoid it by wearing a mask
2. it is a theory that uses Taylor series expansion of the exact equation of states for a gas with $p$ as the variable used in the development
3. it is a theory that uses Taylor series expansion of the exact equation of states for a gas with $V$ as the variable used in the development
4. it is a theory that uses Taylor series expansion of the exact equation of states for a gas with $T^{-1}$ as the variable used in the development
5. it is a theory that uses Taylor series expansion of the exact equation of states for a gas with $V^{-1}$ as the variable used in the development

Hint

Find the answer keys on this page: Answers to selected test your knowledge questions. Don’t cheat! Try solving the problems on your own first!

Homework Assignment

Solve the following problems from the textbook: